人体运动目标的检测与跟踪技术是计算机视觉的主要研究方向之一,在生物医学,人机交互,虚拟现实,智能安全监控,机器人技术,图像压缩,计算机图形学等领域都有着广泛的应用。
运动目标的检测就是从视频流中去除静止的背景,检测出运动的目标及携带的运动信息,运动目标的检测对跟踪等后期处理非常关键[1]。目前,运动目标的检测方法主要有四种:背景差分法、帧间差分法、光流法、基于特征的方法。
现有的目标跟踪方法主要有两类:一类是基于相关的目标跟踪。这是一种先检测后跟踪的方法,它适用于目标之间相互作用较小和背景较简单的情况 ;另一类是基于特征的目标跟踪。这是一种先跟踪后检测的方法,跟踪的结果需要检测来校正[2]。
基于特征的目标跟踪最常用的方法是卡尔曼滤波器,但该算法要求系统是线性高斯型的,而对于人体运动来说是非线性非高斯的,所以不能直接用来解决人体目标跟 踪问题。为此,人们开发出各种非线性滤波算法。一种是扩展卡尔曼滤波算法(EKF),它对非线性系统进行局部线性化,从而间接利用卡尔曼滤波算法进行滤波 与估算,只适用于滤波误差和预测误差很小的情况;另一种是基于蒙特卡罗算法的粒子滤波器(PF),在非线性非高斯系统中表现出来的优越性,决定了其应用范 围非常广泛。粒子滤波技术通过非参数化的蒙特卡罗模拟方法来实现递推运算的贝叶斯滤波,能适用于任何用传统的状态空间模型以及卡尔曼滤波模型表示的非线性 系统,精度可以逼近最优估计 [3]。
1 系统设计描述
系统流程如图1,在摄像机静止的情况下,本文首先采用DirectShow技术读取视频流,并对场景进行初始化,利用初始不含前景的连续N帧图像构造初始 的背景模型,然后根据一定的刷新速度更新背景模型,使它能够适应缓慢的光照变化。当有运动目标出现时系统立即用背景差分法进行检测,如果差值象素面积大于 阈值说明是前景(否则重新检测)可检测到运动区域的大小和形心坐标(x,y), 在一定的时间间隔 t(t<<1s)后,再次利用背景差分法检测运动区域,如果差值象素面积小于阈值,说明运动物体刚进入就消失了,这可能是光线的剧变或强烈的 干扰,跟踪结束,等待目标进入监控区域。 否则在视频图像中可检测到当前帧的运动区域的形心坐标(x’ y’)。由两个形心坐标(x,y)和( x’ y’)。可算出运动物体的初始速度 ,再通过粒子滤波器技术利用背景差分法检测和运算得到的目标区域的大小、形心坐标、初始速度三个参数建立跟踪模型,对运动目标进行跟踪,直到运动目标离开监控区域。
,再通过粒子滤波器技术利用背景差分法检测和运算得到的目标区域的大小、形心坐标、初始速度三个参数建立跟踪模型,对运动目标进行跟踪,直到运动目标离开监控区域。
该方法很好的解决了人体目标跟踪问题,可广泛应用于非线性非高斯系统。
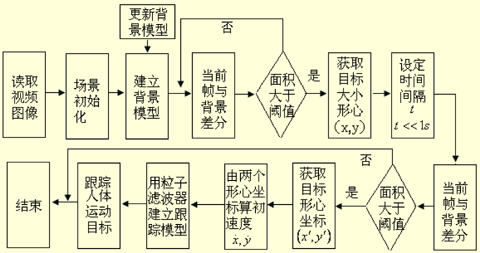
图1 系统流程
2 人体运动目标的检测
2.1 背景模型
背景差分法是目前运动目标检测中最常用的一种方法,它是利用当前图像与背景模型图像相差分并阈值化后检测出运动物体的一种技术。该算法的公式及流程图(如图2)表示如下:
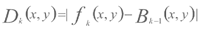 (1)
(1)
 (2)
(2)
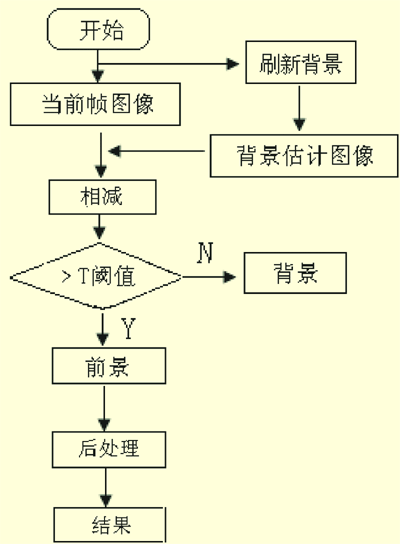
图2 背景差分法流程图
该方法的基本思想是将当前帧图像fk与事先存储或者实时得到的背景图像Bk-1相减,若象素差值Dk大于某一阈值T,则判定此象素为运动目标上的象素,否则为背景象素点,阈值操作后的结果直接给出了对象的位置、大小、形状等信息。背景差分法的效果图如图3所示。

背景图像 目标图像 前景图像 运动目标
图3 背景差分法的效果图
背景差分法的优点是算法容易实现,速度快,检测效果较好,能够提供运动目标最完全的特征数据,缺点是对户外日照、室内灯光渐变和其它外来无关事件的干扰等特别敏感。因此我们需要对背景模型进行更新。
2.2 自适应背景更新[4]
由于背景差分法存在上述缺点,在这里我们采用文献[4]中的方法对背景进行实时更新。
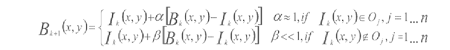 (3)
(3)
其中Ik表示当前图像,Bk表示当前背景,Bk+1是下一帧的背景,Qj是第j个运动目标,n是第k帧运动目标的总个数。 和
和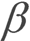 取值范围在[0,1]。若当前象素点属于目标,
取值范围在[0,1]。若当前象素点属于目标, 取接近于1,此处背景不更新,Bk+1(x,y)≈Bk(x,y)。若当前象素点不属于目标,取
取接近于1,此处背景不更新,Bk+1(x,y)≈Bk(x,y)。若当前象素点不属于目标,取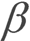 接近于0,此处背景更新为当前帧对应象素值,Bk(x,y)≈Ik(x,y)。
接近于0,此处背景更新为当前帧对应象素值,Bk(x,y)≈Ik(x,y)。
2.3 利用背景差分法获取运动目标参数
当物体进入监控区域时,系统对运动目标进行检测,在第一次用背景差分法检测到前景时(其面积大于给定阈值)用图4中A表示,可获取运动物体的尺寸和形心坐 标(x,y),在时间间隔t(t<<1s)后,再次运用背景差分法获取前景,可用图4中B表示,形心坐标为(x’ y’)。物体的初始速度表示如下:
 (4)
(4)

图4 背景差分法获取参数简图
3 人体运动目标的跟踪
3.1 粒子滤波器
蒙特卡罗方法是一种用采样的方法解决难以处理的积分,尤其是对高维积分处理的方法。该方法将系统状态的后验分布由一组带有权重的离散采样来表达,并通过这些带有权重的离散粒子来估计系统状态[5]。
在k时刻后验密度可以近似表示为:
 (5)
(5)
当 时,估计式(5)接近于真实的后验概率密度
时,估计式(5)接近于真实的后验概率密度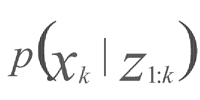 [6]。
[6]。
在粒子滤波算法中存在着粒子退化现象,即当迭代一定次数后,除一个“粒子”外,其余“粒子”的权值都趋于零。而且这个“粒子”的权值只会随时间推移而增大,因此,退化问题是不可避免的。这里我们用表示“退化”程度的度量,它的近似值为
 (6)
(6)
由以上定义可得,Neff≦Ns,Neff越小,退化越严重[7,8,9]。
粒子滤波器的算法如下:

采样
根据式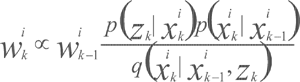 更新权值
更新权值
END FOR
归一化权值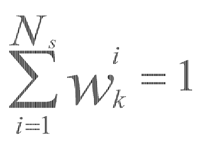
IF 式(6)值太小,说明了退化严重。
重采样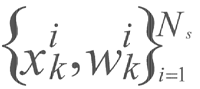
END IF
3.2 人体运动目标跟踪模型
在本文中,人体运动目标可用矩形模板 来表示。并利用背景差分法所检测和计算得到的参数来建立跟踪模型。 (x,y)表示形心坐标,
来表示。并利用背景差分法所检测和计算得到的参数来建立跟踪模型。 (x,y)表示形心坐标, 为点的速度,a,b为矩形的宽度和高度。目标状态向量表示为
为点的速度,a,b为矩形的宽度和高度。目标状态向量表示为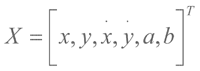 ,状态转移模型建立如:
,状态转移模型建立如: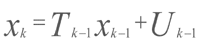 (7)
(7)
Tk-1为状态转移矩阵。在本文的人体目标跟踪实验中Tk-1的初值确定可用文献[2]中的方法,(x,y  )表示人体的运动,其时间进化模型采用均速直线运动模型,a,b可采用静止模型,状态的改变由噪声驱动。状态转移矩阵Tk-1可用如下矩阵表示:
)表示人体的运动,其时间进化模型采用均速直线运动模型,a,b可采用静止模型,状态的改变由噪声驱动。状态转移矩阵Tk-1可用如下矩阵表示:
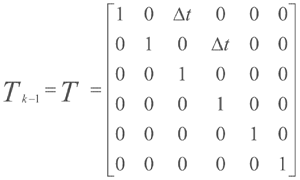
 表示系统状态噪声,初始值△t=1。观测向量
表示系统状态噪声,初始值△t=1。观测向量 ,其中x’ y’分别是目标形心轴上位置的观测值。观测模型可建立为
,其中x’ y’分别是目标形心轴上位置的观测值。观测模型可建立为 (8)
(8)
 ,为高斯零均值白噪声。初始概率密度
,为高斯零均值白噪声。初始概率密度 ,粒子个数N=1000。
,粒子个数N=1000。
4 粒子滤波器的应用
利用本文建立的目标状态转移模板和观测模板所组成的粒子滤波模型,对户外场景进行了单个人体运动的目标跟踪实验。在实验中我们采用型号为PK-83摄像头 采集了350帧的视频序列。计算机配置采集卡,跟踪分辨率为320×240的图像序列。本文用VC++编 程实现算法,粒子滤波器的跟踪结果用红色矩形框表 示。通过实验可见,在目标跟踪视场内包括摆动的树,树的阴影及非常强的照明等干扰和遮挡因素,该系统仍然可以成功的跟踪运动目标。在图5中显示第46、 72、98、156、200、220、250、298帧跟踪的结果。在第156帧中运动目标进入了遮挡区,滤波器的跟踪效果仍然很好;在第200帧中,虽 然运动目标已经出了遮挡区系统仍在继续跟踪。为了解决退化问题,我们适当增加了粒子数目,并通过对 做N次采样,重新生成一组新样本集
做N次采样,重新生成一组新样本集 ,为每一个样本赋予相等的权值1/Ns。减少了权值太小的粒子,集中关注权值大的粒子,从而改善了系统的实时性。
,为每一个样本赋予相等的权值1/Ns。减少了权值太小的粒子,集中关注权值大的粒子,从而改善了系统的实时性。

(1)第46 帧 (2)第72帧 (3)第98帧 (4)第156帧

(5)第200帧 (6)第220帧 (7)第250帧 (8)第298帧
图5 基于粒子滤波器的人体目标跟踪结果
5 结论
本文运用粒子滤波器算法根据背景差分法所检测和计算得到的参数来建立跟踪模型。该算法解决了跟踪目标中的非线性非高斯难题,克服了卡尔曼滤波和扩展卡尔曼 滤波在人体运动目标跟踪上的缺陷。对于本文跟踪实验过程中有活动目标干扰、并且目标暂时地被遮挡后又重新出现的情况,该算法仍能正确地进行状态跟踪。实验 结果表明了该算法具有良好的鲁棒性。该方法用在户外环境下能很好地检测出运动目标,噪声抑制能力强。可广泛应用于航空器位置的跟踪、噪声环境通信信号的估 计、人体或车辆的跟踪。
作者:
张铁力 (1981—)
男,黑龙江牡丹江人,硕士研究生,研究方向为计算机视觉分析及人工智能。
其它作者:
王然冉 (1962—),男,辽宁沈阳人,副教授,研究生导师,研究方向为视频图像分析识别和多媒体、流媒体软件编程;
李晓佳 (1983—),女,黑龙江肇东人,硕士研究生。研究方向为现场总线技术及智能控制。
参考文献:
[1] 曹丽,王亚明,周维达等.基于动态图像序列的运动目标检测与跟踪[J].计算机仿真,2006,23(5):194-196.
[2] 王长军,朱善安.基于视频的目标检测与跟踪技术研究[D].博士学位论文,浙江大学,2006.4:77-89.
[3] 方帅,迟健男,徐心和.视频监控中的运动目标跟踪算法[J].控制与决策,2005,20(12):1388-1391.
[4] 刘雪,王华杰,常发亮.视频图像序列中运动目标的 提取与跟踪[J].仪器仪表与检测技术,2007,26(1):102-103.
[5] 江宝安,卢焕章. 粒子滤波器及其在目标跟踪中的应用[J].雷达科学与技术,2003,1(3):170-174.
[6] Bergman,N.,A. Doucet,and N. Gordon.Optimal estimation and Cramer-Rao bounds for partial non-Gaussian state space models[J]. Ann. Inst. Statist. Math, 2001,53(l):97-112.
[7] LI Yan-qiu,SHEN Yi,LIU Zhi-yan.A New Particle Filter for Nonlinear Tracking Problems[J].Chinese Journal of aeronautics,2004,17(3):170-175.
[8] 刘大键,朱善安.基于最大后验概率密度的粒子过滤器跟踪算法[J].光电工程,2005,32(11):9-11.
[9] Liu J S,Chen R.Sequential Monte Carlo methods for dynamic systems[J].Journal of the American Statistical Association,1998,93(443):1032-1044.